Trissecção do Ângulo

Este problema se consiste em construir um ângulo com um terço da amplitude de um primeiro ângulo dado, utilizando a régua não-graduada e o compasso.

A origem deste problema é desconhecida. O que se sabe é que a primeira tentativa de resolvê-lo foi feita pelo geômetra Hipias (420 a.C.).

Na Grécia antiga sabia-se como bissectar qualquer ângulo com régua e compasso, seguindo os seguintes passos:

· Construía-se uma circunferência centrada no vértice do ângulo (O).

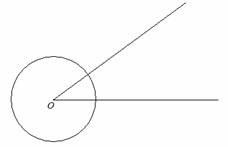
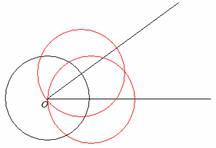
· Construía-se em seguida duas circunferências do mesmo raio centradas nos pontos de intersecção da circunferência anterior com os lados do ângulo.

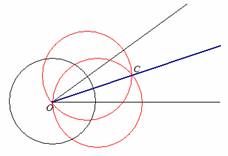
· As duas novas circunferências se intersectam em dois pontos: no vértice do ângulo e num ponto C. A semi-reta com origem no vértice do ângulo e que passa por C divide o ângulo em dois ângulos com a mesma amplitude.

Depois da bissecção, os gregos passaram a procurar soluções para o problema da trissecção. Os gregos sabiam trissectar alguns ângulos (90°, por exemplo), mas não conheciam um método que funcionasse para todos os outros. Hoje em dia, sabemos que um ângulo de 60° não pode ser trissectado usando apenas régua e compasso.

Arquimedes descobriu um processo de se trissectar qualquer ângulo usando compasso e a régua, mas graduada (o que já não convém nos postulados de Euclides). Esse processo se consistia em:

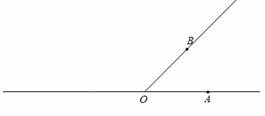
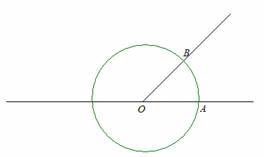
· Construir um ângulo AOB com a mesma amplitude do ângulo dado e tal que a distância de O e B seja igual a distância entre dois pontos marcados na régua (tenha uma medida marcada)

· Construir a circunferência de centro O e que passa por B.

· Colocar um dos pontos marcados na régua num ponto C da reta definida por O e A, colocar o outro ponto marcado num ponto D da circunferência e ter a reta a passar por B.

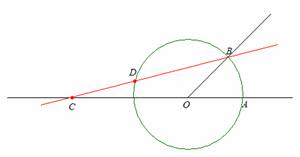
Então o ângulo ACB tem um terço da amplitude do ângulo AOB.

Voltar a OS TRÊS PROBLEMAS CLÁSSICOS DA GEOMETRIA GREGA

Voltar a TÓPICOS DE MATEMÁTICA