Duplicação do Cubo

Este problema se consiste em construir um cubo com o dobro de volume de um primeiro cubo dado, utilizando a régua não-graduada e o compasso.

Existem várias histórias que contam a origem desse problema.

A mais conhecida delas diz que uma grande peste havia afetado a cidade de Atenas, e os habitantes foram até o oráculo da ilha de Delos em busca de auxílio. O oráculo teria dito para se erguer um altar igual ao dobro do já existente, também em formato cúbico, e assim a peste cessaria. Os atenienses logo dobraram as medidas das arestas do cubo:

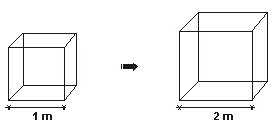
A peste, em vez de acabar, aumentou. Isso porque os gregos cometeram um erro simples: eles simplesmente, ao invés de dobrar, octuplicaram o volume do altar, pois para um cubo de aresta 1 (uma medida qualquer) temos o volume . Mas para um cubo de aresta 2, temos .

Os gregos pensaram que seria fácil a resolução desse problema porque eles pensavam que o poderiam resolver baseando-se em um outro problema que eles bem conheciam: a duplicação do quadrado.

Para duplicarmos um quadrado ABCD, traçamos uma diagonal BD e construímos um quadrado de lado BD. Assim, dado um quadrado de lado a , é possível encontrar um outro quadrado de lado b cuja área seja o dobro do primeiro.

Claro que o problema demorou tanto para ser resolvido que a peste acabou.

O primeiro grande passo nesse problema foi dado por Hipócrates de Chios, provavelmente não muito depois da aparição do problema.

Hoje, esse problema pode ser facilmente formulado pela Álgebra:

Voltar a OS TRÊS PROBLEMAS CLÁSSICOS DA GEOMETRIA GREGA

Voltar a TÓPICOS DE MATEMÁTICA