Exercícios Comentados
ÁLGEBRA
Exercício 1: A expressão algébrica que representa a situação: “o quadrado da soma de
dois números, mais 5 unidades” é:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Resposta: alternativa C
Comentário: O primeiro passo é saber
interpretar o exercício. Ele pede claramente “o quadrado da SOMA de dois
números”, que será ![]() . Somando isto a 5
unidades, temos
. Somando isto a 5
unidades, temos ![]() . Percebemos que nenhuma das outras
alternativas satisfazem ao enunciado proposto.
. Percebemos que nenhuma das outras
alternativas satisfazem ao enunciado proposto.
RAÍZES
Exercício 2: Em um triângulo retângulo, a
hipotenusa mede 14 cm e um dos catetos ![]() . Determine a medida do outro cateto.
. Determine a medida do outro cateto.
Resposta:
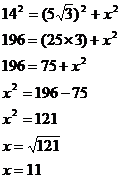
Comentário: Hipotenusa e catetos são termos que
automaticamente nos remetem ao teorema do famoso matemático Pitágoras. O
enunciado desse teorema (certamente um dos mais célebres de toda a Matemática e
o que possui mais demonstrações de todos os teoremas da Matemática) diz que “o
quadrado da hipotenusa é igual a soma dos quadrados
dos catetos”.
Geometricamente falando, sabemos que a hipotenusa é o lado
de um triângulo retângulo que é oposto ao ângulo de 90º graus, e os catetos são
os dois lados adjacentes ao ângulo reto do triângulo retângulo. Assim, temos:
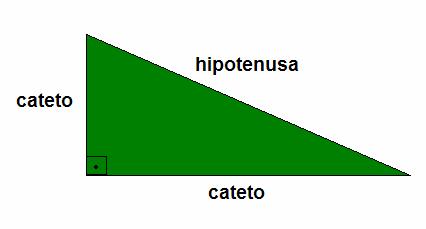
Algebricamente, podemos substituir a hipotenusa por a e os dois catetos por b e c.
Assim, temos a expressão ![]() .
.
No exercício proposto, nos é dado o valor da hipotenusa e de
um dos catetos. Assim sendo, apenas devemos substituir os valores apresentados
na fórmula de Pitágoras e, para o valor do outro cateto, podemos escolher
qualquer incógnita (no caso, x), e
chegaremos ao resultado, que é 11.
Exercício 3:
Observando o retângulo da figura abaixo, determine o perímetro e a área.
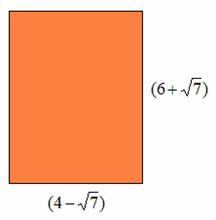
Resposta:
Perímetro
![]()
Área
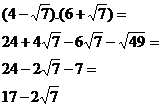
Comentário: Sabemos que o perímetro de um
polígono qualquer é a soma de seus lados. A área do retângulo é igual ao
produto de sua base por sua altura. Basta apenas substituir esses valores e
efetuar os cálculos. É importante lembrar que no cálculo de raízes, devemos
sempre trabalhar com os termos semelhantes, ou seja, raiz subtrai e soma apenas
raiz.
NÚMEROS COMPLEXOS
Exercício 4: Calcule o valor de m e k,
sendo ![]() , para que z seja
um número imaginário puro.
, para que z seja
um número imaginário puro.
Resposta:

Comentário: Relembrando um pouco o conceito de
números complexos, sabemos que, como definição de números complexos, temos a
expressão algébrica ![]() , onde a corresponde a um número real, e b
é a unidade imaginária. Temos como classificar um número complexo em função da
existência de seus termos. Se o real é igual a zero, temos um número imaginário
puro; e na ausência do imaginário, temos um número real.
, onde a corresponde a um número real, e b
é a unidade imaginária. Temos como classificar um número complexo em função da
existência de seus termos. Se o real é igual a zero, temos um número imaginário
puro; e na ausência do imaginário, temos um número real.
O exercício pede que z
seja um número imaginário puro e, portanto, a parte real (5 – 3m) deve ser
igual a zero.
FUNÇÕES
Exercício 5: Construir o gráfico da função linear
![]() .
.
Resposta:
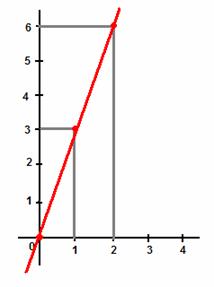
Comentário: Primeiramente, devemos lembrar
alguns conceitos da função linear. Função
linear é uma função do tipo ![]() , onde a é um número real. O gráfico de
qualquer função linear passa obrigatoriamente pelo ponto (0,0), pois se atribuirmos
o valor 0 à incógnita x, teremos 0 vezes um número real, que é igual a 0.
, onde a é um número real. O gráfico de
qualquer função linear passa obrigatoriamente pelo ponto (0,0), pois se atribuirmos
o valor 0 à incógnita x, teremos 0 vezes um número real, que é igual a 0.
Procedemos
da mesma maneira como na função do 1º grau: atribuímos valores a x e formamos os
pares ordenados.
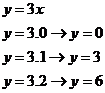
No caso,
escolhemos os valores 0, 1 e 2 para demonstração
apenas.
Agora
traçamos os pares ordenados no plano cartesiano e o gráfico estará pronto.
Voltar a TÓPICOS DE MATEMÁTICA